esemifar

CRAN status Lifecycle: stable

The goal of esemifar is to provide an easy way to estimate the nonparametric trend and its derivatives in trend-stationary, equidistant time series with long-memory stationary errors. The main functions allow for data-driven estimates via local polynomial regression with an automatically selected optimal bandwidth.

Installation

You can install the released version of esemifar from CRAN with:

install.packages("esemifar")

Example 1: Estimation of the nonparametric trend function

This is a basic example which shows you how to solve a common problem. The data airLDN in the package contains daily observations of the air quality index of London (Britain) from 2014 to 2020. The data was obtained from the European Environment Agency. To make use of the esemifar package, it has to be assumed that the data follows an additive model consisting of a deterministic, nonparametric trend function and a zero-mean stationary rest with long-range dependence.

library(esemifar)          # Call the package
data <- airLDN           # Call the 'airLDN' data frame
Yt <- log(data$AQI)      # log-transform the data and store the actual values as a vector 

# Estimate the trend function via the 'esemifar' package
results <- tsmoothlm(Yt, p = 1, qmax = 1, pmax = 1, InfR = "Var")

# Easily access the main estimation results
b.opt <- results$b0             # The optimal bandwidth
trend <- results$ye             # The trend estimates  
resid <- results$res            # The residuals
b.opt
#> [1] 0.2422682
coef(results$FARMA.BIC)         # The model parameters
#>         d        ar 
#> 0.1032687 0.5435804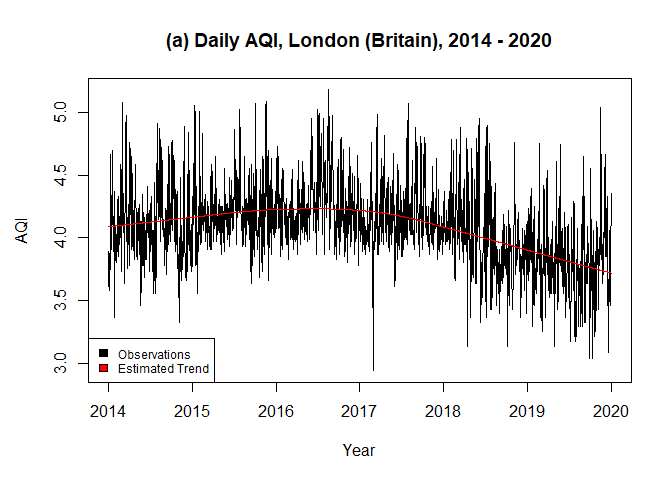

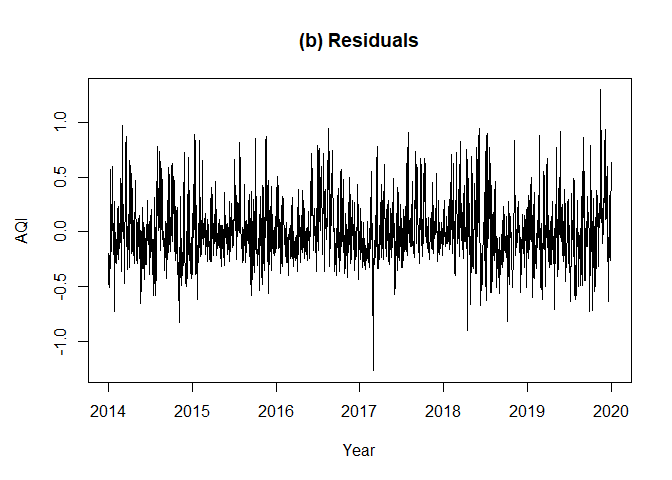
An optimal bandwidth of \(0.2422682\) was selected by the iterative plug-in algorithm (IPI) within tsmoothlm(). A FARIMA (\(1, d, 0\)) was obtained from the trend-adjusted residuals with \(\hat{d} = 0.1032687\) and \(\hat{\phi} = 0.5435804\). Moreover, the estimated trend fits the data suitably and the residuals seem to be stationary.

Example 2: Forecasting capabilities

The trend estimation in combination with a fitted FARIMA model for the trend-adjusted values as in Example 1 is an ESEMIFAR model. With version 2.0.0 of the package, forecasting for based on such fitted ESEMIFAR models can be conducted using a designated predict-method. When applying that method, the user has the option between forecasting intervals based on the normality assumption for the innovations or based on a bootstrap.

h <- 200

# Via a bootstrap
set.seed(123)
fc <- predict(results, n.ahead = h, method = "boot")
head(fc$mean, 2)
#> [1] 4.135976 3.995659
head(fc$lower, 2)
#>           95%      99%
#> [1,] 3.725928 3.534129
#> [2,] 3.510523 3.330463
head(fc$upper, 2)
#>           95%      99%
#> [1,] 4.589879 4.749304
#> [2,] 4.531115 4.723409

# Under normality
fc <- predict(results, n.ahead = h, method = "norm")
head(fc$mean, 2)
#> [1] 4.135976 3.995659
head(fc$lower, 2)
#>           95%      99%
#> [1,] 3.717548 3.586068
#> [2,] 3.497323 3.340734
head(fc$upper, 2)
#>           95%      99%
#> [1,] 4.554404 4.685883
#> [2,] 4.493994 4.650583

Moreover, a quick plot of the results can be generated using a designated plot-method.

t_step <- diff(tail(t, 2))
t2 <- c(t, seq(from = tail(t, 1) + t_step, by = t_step, length.out = h))
plot(fc, t = t2, xlab = "Year", ylab = "AQI",
     main = "Point forecasts with 95%- and 99%-forecasting intervals")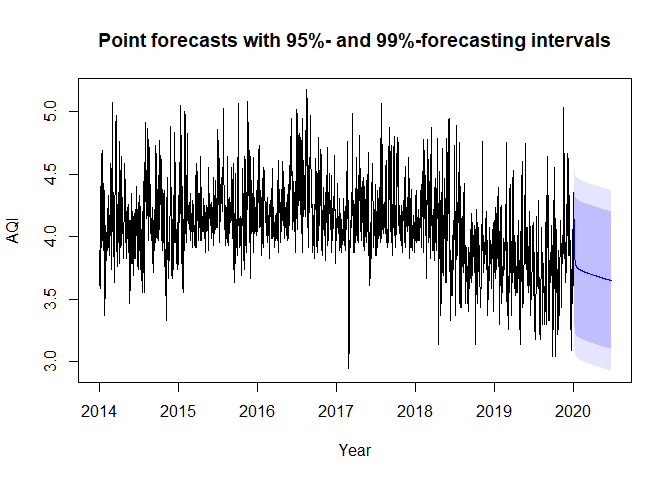

Further applications

The trend estimation function can also be used for the implementation of semiparametric generalized autoregressive conditional heteroskedasticity (Semi-GARCH) models with long memory in Financial Econometrics (see Letmathe et al., 2023).

Functions

In esemifar three functions are available.

Original functions since version 1.0.0:

Original functions since version 2.0.0:

Data sets