The relliptical R package

The relliptical R package offers random numbers generation from members of the truncated multivariate elliptical family of distribution such as the truncated versions of the Normal, Student-t, Laplace, Pearson VII, Slash, Logistic, Kotz-type, among others. Particular distributions can be provided by specifying the density generating function. It also computes the first two moments (covariance matrix as well) for some particular distributions. For more details see (Valeriano, Galarza, and Matos 2023).

Next, we will show the functions available in the package.

Sampling random numbers

The function rtelliptical generates observations from a truncated multivariate elliptical distribution with location parameter mu, scale matrix Sigma, lower and upper truncation points lower and upper via Slice Sampling algorithm (Neal 2003) with Gibbs sampler (Robert and Casella 2010) steps. The dist argument represents the truncated distribution to be used. The values are Normal, t, Laplace, PE, PVII, Slash, and CN, for the truncated Normal, Student-t, Laplace, Power Exponential, Pearson VII, Slash, and Contaminated Normal distributions, respectively.

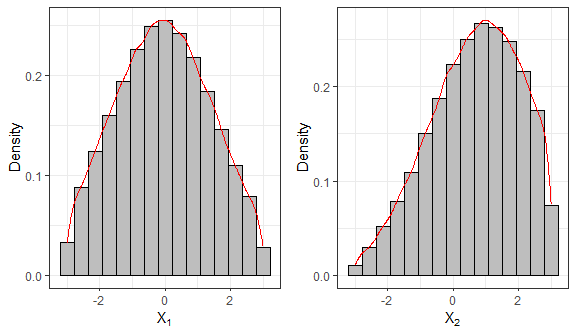
In the following example, we generate \(n = 10^5\) samples from the truncated bivariate Normal distribution.

library(relliptical)

# Sampling from the Truncated Normal distribution
set.seed(1234)
mu  = c(0, 1)
Sigma = matrix(c(3,0.6,0.6,3), 2, 2)
lower = c(-3, -3)
upper = c(3, 3)
sample1 = rtelliptical(n=1e5, mu, Sigma, lower, upper, dist="Normal")
head(sample1)
#>            [,1]       [,2]
#> [1,]  0.6643105  2.4005763
#> [2,] -1.3364441 -0.1756624
#> [3,] -0.1814043  1.7013605
#> [4,] -0.6841829  2.4750461
#> [5,]  2.0984490  0.1375868
#> [6,] -1.8796633 -1.2629126

library(ggplot2)
# Histogram and density for variable 1
f1 = ggplot(data.frame(sample1), aes(x=X1)) + 
  geom_histogram(aes(y=after_stat(density)), colour="black", fill="grey", bins=15) +
  geom_density(colour="red") + labs(x=bquote(X[1]), y="Density") + theme_bw()

# Histogram and density for variable 2
f2 = ggplot(data.frame(sample1), aes(x=X2)) + 
  geom_histogram(aes(y=after_stat(density)), colour="black", fill="grey", bins=15) +
  geom_density(colour="red") + labs(x=bquote(X[2]), y="Density") + theme_bw()

library(gridExtra)
grid.arrange(f1, f2, nrow=1)

This function also allows generating random numbers from other truncated elliptical distributions not specified in the dist argument, by supplying the density generating function (DGF) through arguments either expr or gFun. The DGF must be a non-negative and strictly decreasing function on \((0, \infty)\). The easiest way is to provide the DGF expression to argument expr as a character. The notation used in expr needs to be understood by package Ryacas0 and the environment of R. For instance, for the DGF \(g(t)=e^{-t}\), the user must provide expr = "exp(1)^(-t)". See that the function must depend only on variable \(t\), and any additional parameter must be passed as a fixed value. For this case, when a character expression is provided to expr, the algorithm tries to compute a closed-form expression for the inverse function of \(g(t)\), however, this is not always possible (a warning message is returned).

The following example draws random variates from a truncated bivariate Logistic distribution, whose DGF is given by \(g(t) = e^{-t}/(1+e^{-t})^2, t \geq 0\), see (Fang, Kotz, and Ng 2018).

# Sampling from the Truncated Logistic distribution
mu  = c(0, 0)
Sigma = matrix(c(1,0.70,0.70,1), 2, 2)
lower = c(-2, -2)
upper = c(3, 2)
# Sample autocorrelation with no thinning
set.seed(5678)
sample2 = rtelliptical(n=1e4, mu, Sigma, lower, upper, expr="exp(1)^(-t)/(1+exp(1)^(-t))^2")
tail(sample2)
#>                [,1]       [,2]
#>  [9995,] -0.5639346 -1.4225548
#>  [9996,] -0.4747796 -1.1890135
#>  [9997,] -0.2596561 -0.1126482
#>  [9998,] -1.1517285 -0.9875129
#>  [9999,] -0.9268744 -1.5526844
#> [10000,] -1.1763390 -1.3098489

If it was no possible to generate random samples by passing a character expression to expr, the user may provide a custom R function to the gFun argument. By default, its inverse function is approximated numerically, however, the user may also provide its inverse to the ginvFun argument to gain some computational time. When gFun is provided, arguments dist and expr are ignored.

In the next example, we will draw samples from the truncated Kotz-type distribution, whose DGF is given by

\[g(t) = t^{N-1} e^{-r t^s}, \quad t\geq 0, \quad r>0, \quad s>0, \quad 2N+p>2.\]

As required, this function is strictly decreasing when \((2-p)/2 < N \leq 1\), see (Fang, Kotz, and Ng 2018).

# Sampling from the Truncated Kotz-type distribution
set.seed(9876)
mu  = c(0, 0)
Sigma = matrix(c(1,0.70,0.70,1), 2, 2)
lower = c(-2, -2)
upper = c(3, 2)
sample4 = rtelliptical(n=1e4, mu, Sigma, lower, upper, gFun=function(t){ t^(-1/2)*exp(-2*t^(1/4)) })
f1 = ggplot(data.frame(sample4), aes(x=X1, y=X2)) + geom_point(size=0.50) +
     labs(x=expression(X[1]), y=expression(X[2]), subtitle="Kotz(2,1/4,1/2)") + theme_bw()

library(ggExtra)
ggMarginal(f1, type="histogram", fill="grey")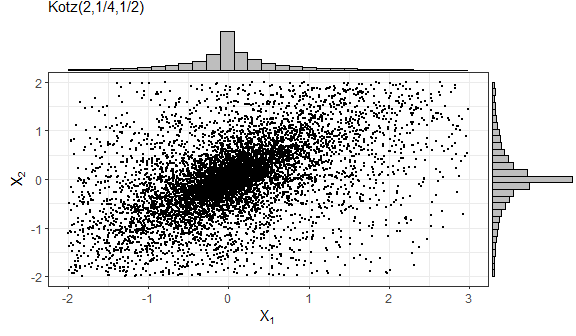

Since the generating process uses an MCMC method, observations will be correlated, so it may be of interest to study some ACF plots. Now, we study the sample from the bivariate logistic distribution.

grid.arrange(grobs=acf.plot(sample2), top="Sample ACF with no thinning", nrow=1)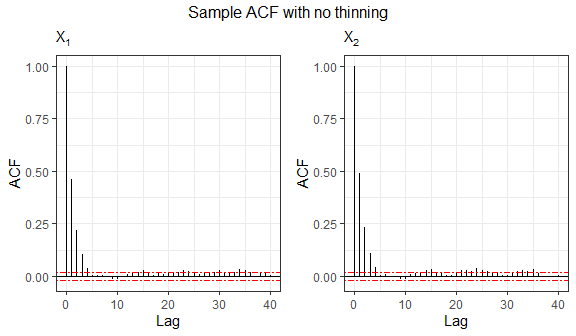

Autocorrelation can be decimated by setting the thinning argument. The thinning factor reduces the autocorrelation of the random points in the Gibbs sampling process. Thinning consists in picking separated points from the sample, at each k-th step. As natural, this value must be an integer greater than or equal to 1.

# Sample autocorrelation with thinning = 3
set.seed(8768)
sample3 = rtelliptical(n=1e4, mu, Sigma, lower, upper, dist=NULL, expr="exp(1)^(-t)/(1+exp(1)^(-t))^2", 
                       thinning=3)
grid.arrange(grobs=acf.plot(sample3), top="Sample ACF with thinning = 3", nrow=1)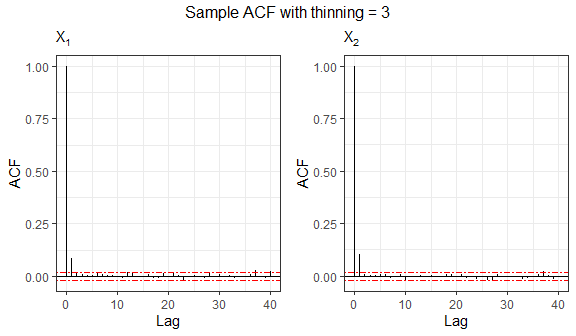

Mean and variance-covariance matrix

For this purpose, we call the function mvtelliptical(), which returns the mean vector and variance-covariance matrix for some specific truncated elliptical distributions. The argument dist sets the distribution to be used and accepts the same values Normal, t, Laplace, PE, PVII, Slash, and CN as before. Moments are computed through Monte Carlo method for the truncated variables and using properties of the conditional expectation for the non-truncated variables.

Next, we compute the moments for a random variable \(X\) following a truncated 3-variate Student-t distribution with \(\nu=0.8\) degrees of freedom. We will consider two scenarios: a first one with only one doubly truncated variable, and a second one with two doubly truncated variables.

# Truncated Student-t distribution
set.seed(5678)
mu    = c(0.1, 0.2, 0.3)
Sigma = matrix(data = c(1,0.2,0.3,0.2,1,0.4,0.3,0.4,1), nrow=length(mu), ncol=length(mu), byrow=TRUE)

# Example 1: one doubly truncated student-t (nu = 0.80)
a = c(-0.8, -Inf, -Inf)
b = c(0.5, 0.6, Inf)
mvtelliptical(a, b, mu, Sigma, "t", 0.80)
#> $EY
#>             [,1]
#> [1,] -0.11001805
#> [2,] -0.54278399
#> [3,] -0.01119847
#> 
#> $EYY
#>            [,1]       [,2]       [,3]
#> [1,] 0.13761136 0.09694152 0.04317817
#> [2,] 0.09694152        NaN        NaN
#> [3,] 0.04317817        NaN        NaN
#> 
#> $VarY
#>            [,1]       [,2]       [,3]
#> [1,] 0.12550739 0.03722548 0.04194614
#> [2,] 0.03722548        NaN        NaN
#> [3,] 0.04194614        NaN        NaN

# Example 2: considering nu = 0.80 and two doubly truncated variables
a = c(-0.8, -0.70, -Inf)
b = c(0.5, 0.6, Inf)
mvtelliptical(a, b, mu, Sigma, "t", 0.80) # By default n=1e4
#> $EY
#>             [,1]
#> [1,] -0.08566441
#> [2,]  0.01563586
#> [3,]  0.19215627
#> 
#> $EYY
#>             [,1]        [,2]       [,3]
#> [1,] 0.126040187 0.005937196 0.01331868
#> [2,] 0.005937196 0.119761635 0.04700108
#> [3,] 0.013318682 0.047001083 1.14714388
#> 
#> $VarY
#>             [,1]        [,2]       [,3]
#> [1,] 0.118701796 0.007276632 0.02977964
#> [2,] 0.007276632 0.119517155 0.04399655
#> [3,] 0.029779636 0.043996554 1.11021985

As seen for the first scenario, some elements of the variance-covariance matrix are shown as NaN. Those are the cases where the moment does not exist (yes, some elements of the variance-covariance matrix may exist and others may not). It is well know that for a Student-t distribution its second moment exist if \(\nu>2\), however, as studied by (Galarza et al. 2022), this condition is relaxed as the number of dimensions containing only finite truncation limits increases.

It is worth mention that the Student-\(t\) distribution with \(\nu > 0\) degrees of freedom is a particular case of the Pearson VII distribution with parameters \(m > p/2\) and \(\nu^* > 0\) when \(m = (\nu+p)/2\) and \(\nu^* = \nu\).

Finally, for comparison purposes, we compute the moments for a doubly truncated Pearson VII distribution with parameters \(\nu^* = \nu = 0.80\) and \(m = (\nu + 3)/2 = 1.90\), which is equivalent to the Student-t distribution mentioned above. Therefore, their moments should be nearly equal.

# Truncated Pearson VII distribution
set.seed(9876)
a  = c(-0.8, -0.70, -Inf)
b  = c(0.5, 0.6, Inf)
mu = c(0.1, 0.2, 0.3)
Sigma = matrix(data = c(1,0.2,0.3,0.2,1,0.4,0.3,0.4,1), nrow=length(mu), ncol=length(mu), byrow=TRUE)
mvtelliptical(a, b, mu, Sigma, "PVII", c(1.90,0.80), n=1e6) # n=1e6 more precision
#> $EY
#>             [,1]
#> [1,] -0.08558130
#> [2,]  0.01420611
#> [3,]  0.19166895
#> 
#> $EYY
#>             [,1]        [,2]       [,3]
#> [1,] 0.128348258 0.006903655 0.01420704
#> [2,] 0.006903655 0.121364742 0.04749544
#> [3,] 0.014207043 0.047495444 1.15156461
#> 
#> $VarY
#>             [,1]        [,2]       [,3]
#> [1,] 0.121024099 0.008119433 0.03061032
#> [2,] 0.008119433 0.121162929 0.04477257
#> [3,] 0.030610322 0.044772574 1.11482763

References